Tema 2. El trabajo de Galileo

I  CAÍDA LIBRE

El término caída libre es una expresión aplicado tanto a los cuerpos que ascienden como a los que descienden. La caída libre es un movimiento de aceleración constante. 

Se le llama caída libre al movimiento de un objeto o cuerpo en donde no existe resistencia de algún medio. Como sabrás en el movimiento de la caída libre de los cuerpos intervienen varios factores que son: la forma del cuerpo y el medio por el que se desplaza (En el aire, agua, etc.)

Una mejor forma de explicar la caída libre es que si se elimina el medio de resistencia, por ejemplo el aire, y se arroja una pelota y una pluma de un ave, ambos objetos caerán al mismo tiempo sin importar su peso, ya que no existe resistencia alguna sobre éstos.

II  ARISTOTELES

El filósofo griego Aristóteles (348-322 a C) afirmó en sus escritos que los cuerpos caen a una velocidad proporcional a su peso.

Aristóteles formuló su teoría de los objetos en caída libre, suponiendo que todos se componen de cuatro elementos: tierra, aire, fuego y agua. Los que están constituidos primordialmente por tierra y agua tratan de alcanzar su lugar natural de reposo: la Tierra; Los objetos que se componen de aire tratan de subir a su estado natural de reposo: el cielo.

Aristóteles era un filósofo muy respetado; de ahí que hubiera pocos dispuestos a poner en duda sus teorías y conclusiones. Por tal razón, se avanzó poco en muchos siglos en el conocimiento de los cuerpos en caída.

La teoría de Aristóteles se basaba en que todos los cuerpos pesados caían más rápido que los ligeros. Él mencionaba que existían dos tipos de movimientos: naturales, éste a su vez se dividía en dos movimientos que era el movimiento circular de los cosmos y el movimiento hacia la superficie o hacia la atmosfera; y violentos.

El movimiento natural de un cuerpo consistía en la naturaleza formada del mismo (agua, tierra, aire, fuego), éstos se debían mover a su lugar natural y dependiendo del elemento en mayor abundancia era el que determinaba la dirección y la rapidez de éste. Una piedra grande caía más rápido que una piedra pequeña, ya que tenía más tierra.

Los movimientos violentos para Aristóteles eran aquellos que se apartaban de su trayectoria natural. Un ejemplo, que una piedra se elevara hacia atmosfera, cuando su lugar natural es la superficie.

Aristóteles también en sus estudios realizados decía que la rapidez de la caída los cuerpos era directamente proporcional a su peso y que conforme se acercara a su lugar natural su velocidad aumenta.

La teoría propuesta por Aristóteles podía parecer lógica pues un cuerpo pesado cae más rápido que un ligero, ya que la gravedad lo atrae con mayor fuerza. Pero sus argumentos no eran suficientes para poder afirmarlo, sin embargo en su momento fue la mejor manera de explicar la caída libre.

II Galileo Galilei.

Fue el célebre italiano Galileo Galilei quien rebatió la concepción de Aristóteles al afirmar que, en ausencia de resistencia de aire, todos los objetos caen con una misma aceleración uniforme. Pero Galileo no disponía de medios para crear un vacío succionando el aire. 

Las primeras máquinas neumáticas capaces de hacer vacío se inventaron después, hacia el año 1650. 

Tampoco disponía de relojes suficientemente exactos o de cámaras fotográficas de alta velocidad. Sin embargo, ingeniosamente probó su hipótesis usando planos inclinados, con lo que conseguía un movimiento más lento, el que podía medir con los rudimentarios relojes de su época. Al incrementar de manera gradual la pendiente del plano dedujo conclusiones acerca de objetos que caían libre mente.En el año 1971 un astronauta realizó en la Luna, donde no existe atmósfera, el experimento de soltar desde una misma altura y simultáneamente un martillo y una pluma. Ambos objetos hicieron contacto con la superficie lunar al mismo tiempo. Cuando se emplea el término objeto en caída libre se incluye  tanto el soltar como el lanzar hacia arriba o hacia abajo el objeto. Cualquier objeto que cae libremente tiene una aceleración dirigida hacia abajo, independientemente del movimiento inicial del objeto. La magnitud de esta aceleración de caída libre se denota con el símbolo g, cuyo valor varía ligeramente con la altura y con la latitud. En la cercanía de la

superficie de la Tierra el valor de g es aproximadamente 9,8 m/s². Ahora, la causa de esta aceleración fue encontrada por Newton, quien estableció en su ley de Gravitación Universal que las masasse atraen en proporción directa al producto de sus masas e

invers amente a su separación al cuadrado. Es la masa de la Tierra

la que origina esta aceleración de 9,8 m/s² en su superficie. La caída libre es un ejemplo común de movimiento uniforme-mente acelerado, con una aceleración a = -9,8 m/s². El signo 

menos indica que la aceleración está dirigida en sentido contrario al eje en dirección vertical (eje apuntando verticalmente hacia arriba). Si se escoge el eje vertical en dirección hacia la Tierra, la aceleración se toma como a = +9,8 m/s². Las ecuaciones cinemáticas para el movimiento en una línea 

recta bajo la aceleración de gravedad son las mismas que para cualquier movimiento con aceleración constante:

El subíndice i denota cantidades iniciales, g la aceleración de

gravedad y t, el tiempo.

Uno de los grandes aportes que hay en la Física, es sin duda alguna el que realizó el científico Galileo Galilei que demostró que en todos los cuerpos la aceleración de la gravedad, es igual sin importar su peso, en otras palabras, todos los cuerpos caen al mismo tiempo sin importar su peso.

Esto lo pudo comprobar con su experimento realizado desde la Torre de Pisa. Galileo arrojó dos objetos de diferente peso y mostró que caían al mismo tiempo.

Actualmente, se cree por parte de historiadores que éste experimento de Galileo en la Torre de Pisa no lo pudo llevar a cabo, debido a la dificultad de medir el tiempo. Sin embargo, Galileo Galilei realizó otro experimento llamado Planos inclinados y en ambos experimentos pudo llegar a la misma conclusión. Él utilizó planos inclinados y dos esferas de distinto peso, estudió detalladamente el comportamiento de las esferas sobre los planos inclinados y notó que a pesar de que las esferas eran de distinto peso su comportamiento sobre ellos no difiere. El objetivo de haber utilizado los planos inclinados era que gracias a su superficie hace que los objetos se muevan más lento y que se pueda medir mejor el tiempo de caída. Galileo utilizó para éste experimento un reloj de agua, clepsidra.

En la teoría de Galilei él explica que si dos cuerpos de diferente peso caían desde el vacío en donde no hay aire, ambos caerían al mismo tiempo. No obstante, Galileo no contaba con un vacío pero pudo imaginar uno. Él dibujo un cuerpo pesado atado a un cuerpo ligero y dedujo que éste cuerpo compuesto caerían más rápido que el cuerpo pesado solo, y que el cuerpo ligero no podía retardar su caída sino que caía con más velocidad.

Sin duda alguna, las afirmaciones en la teoría de Galileo Galilei pudieron corregir la idea que se tenía durante mucho tiempo de la caída libre que descubrió Aristóteles.

III Aportaciones de Galileo en la construcción

 de conocimiento científico.

Galileo unió la física con la matemática. Desde Galileo se encuentran ecuaciones matemáticas en los textos físicos. Encontró por ejemplo que si la acelación era constante, la distancia recorrida era proporcional al cuadrado del tiempo. Tambien aportó la descripción moderna del movimiento en un sistema de referencia.

Galileo realizó notables aportaciones científicas en el campo de la física, que pusieron en entredicho teorías consideradas verdaderas durante siglos. Así, por ejemplo, demostró la falsedad del postulado aristotélico que afirmaba que la aceleración de la caída de los cuerpos -en caída libre- era proporcional a su peso, y conjeturó que, en el vacío, todos los cuerpos caerían con igual velocidad. Para ello hizo deslizar esferas cuesta abajo por la superficie lisa de planos inclinados con distinto ángulo de inclinación (y no fue con el lanzamiento de cuerpos de distinto peso, desde la torre inclinada de Pisa, como se había creído durante mucho tiempo).

Entre otros hallazgos notables figuran las leyes del movimiento pendular (sobre el cual comenzó a pensar, según la conocida anécdota, mientras observaba una lámpara que oscilaba en la catedral de Pisa), y las leyes del movimiento acelerado.

Sus aportaciones en el terreno de la astronomía y el estudio del universo no fueron menos importantes. A principios del siglo XVII, perfeccionó el catalejo, un instrumento óptico de reciente invención, para obtener un telescopio de sesenta aumentos.

Con la ayuda de dicho aparato, Galileo exploró el cielo y llegó a conclusiones que revolucionaron profundamente la manera de entender el orden del universo. En contra de la creencia general, demostró que la superficie de la Luna no era cristalina, sino que estaba cubierta de cráteres y montañas, con lo que refutó la idea aristotélica de la absoluta perfección de los astros. De la misma manera, descubrió las manchas solares, con lo que pudo determinar el período de rotación del Sol y la dirección de su eje. Galileo descubrió, asimismo, los cuatro satélites mayores de Júpiter y demostró que no todos los astros giraban alrededor de la Tierra. Esta constatación de las teorías copernicanas, contraria a la cosmología de Tólomeo vigente hasta entonces, le valió la condena de las autoridades eclesiásticas, pero desempeñó un papel fundamental para edificar la moderna visión del universo.

Puede considerarse a Galileo como el fundador de la astronomía moderna, y más en general, como el introductor del método experimental en la investigación científica. Además de sus extraordinarios resultados como físico y astrónomo, la importancia de Galileo está precisamente en haber creado una mentalidad científica nueva, cuyas bases son aún las nuestras. Por estos motivos, puede considerarse a Galileo como el fundador de la ciencia moderna, basada en la observación de los hechos, la realización de experimentos y la formulación de teorías explicatorias. En la historia de la cultura, Galileo se ha convertido en el símbolo de la lucha contra la autoridad y de la libertad en la investigación.

Sus dos principales obras fueron Diálogos relacionados con los dos grandes sistemas del mundo y Diálogos relacionados con dos nuevas ciencias. El primero de ellos, que Galileo terminó de escribir en 1630, fue el que desencadenó su persecución y condena por la Inquisición. La publicación del segundo libro se produjo en 1638. Como veremos, Galileo apoyó la visión heliocéntrica, y aportó nuevas ideas sobre el movimiento de los cuerpos.

Inercia y relatividad. Para comprender mejor las ideas de Galileo, es imprescindible referirse previamente a la obra de Nicolás Copérnico. En su trabajoSobre las revoluciones de las esferas celestes, publicado en 1543, desarrolló un modelo en el que el Sol está inmóvil en el centro del universo y los planetas giran alrededor de él. Este sistema heliocéntrico permite explicar de manera muy sencilla algunos aspectos del movimiento de los planetas, como por ejemplo su movimiento retrógrado: dado que los planetas giran alrededor del Sol con distintos períodos, las posiciones y velocidades relativas a la Tierra puede cambiar en distintas épocas del año, y su movimiento aparente puede ser “hacia atrás”. En el sistema geocéntrico de Tolomeo, para explicar este movimiento aparente era necesario suponer que los planetas realizaban complicadísimas trayectorias, conteniendo epiciclos a lo largo de sus trayectorias circulares.

Es importante destacar que a los efectos de lo que hoy llamaríamos una descripción cinemática del sistema solar, ambos puntos de vista son perfectamente adecuados. En un sistema de referencia fijo a la Tierra, la trayectoria del Sol y el resto de los planetas es muy complicada. Sin embargo, en un sistema de referencia fijo al Sol, la descripción es mucho más sencilla.

Galileo adhirió a la visión copernicana, seguramente influido por los descubrimientos que realizó partir de 1609. Efectivamente, realizando observaciones con un telescopio, estudió la forma y superficie de la Luna, descubrió lunas en otros planetas y encontró diferencias entre los planetas y las estrellas, que mostraban inequívocamente que las estrellas se encontraban a distancias mucho mayores.

La Tierra se desplaza velozmente alrededor del Sol, a unos 30 km/seg, y además gira sobre su eje, de manera que un punto sobre la superficie del ecuador se mueve respecto al eje de rotación a unos 500 m/seg. ¿Por qué no nos damos cuenta de esos movimientos? Aquí es donde la descripción del movimiento galileana se relaciona con el “sistema del mundo”. Hasta antes de Galileo, uno de los argumentos para asegurar la inmovilidad de la Tierra era que, si esta se moviese, un objeto lanzado verticalmente hacia arriba no debería volver a caer en el punto de lanzamiento, ya que la Tierra se desplazaría durante el tiempo que tarda el vuelo del objeto lanzado.

Manuscrito de Galileo sobre el movimiento de los proyectiles

Para Galileo, el estado “natural” de movimiento de un cuerpo es el de mantener su velocidad. Si inicialmente está en reposo se mantendrá en reposo. Pero si inicialmente se mueve con una cierta velocidad no nula, y si no está sometido a ninguna acción externa, mantendrá su velocidad constante. Este es el principio de inercia que luego Newton utilizaría en sus Principia. Consecuentemente, un objeto lanzado verticalmente hacia arriba desde la Tierra tiene inicialmente la misma velocidad horizontal que la Tierra, y por lo tanto su movimiento a lo largo de la horizontal acompañará al de la Tierra.

IV ACELERACIÓN; DIFERENCIA CON 

VELOCIDAD.

I ACELERACIÓN.

La aceleración es la acción y efecto de acelerar (aumentar la velocidad). El término también permite nombrar a la magnitud vectorial que expresa dicho incremento de la velocidad en una unidad de tiempo (metro por segundo cada segundo, de acuerdo a su unidad en el Sistema Internacional).

El concepto aceleración, no tiene que ver con ir moviéndose rápido.  Es un concepto que en muchas ocasiones ha sido mal utilizado en la vida real, sin embargo, su significado en física es muy diferente.  Es muy común escuchar que se utiliza este concepto para indicar que un objeto se mueve a gran velocidad lo cual es incorrecto.  El concepto aceleración se refiere al cambio en la velocidad de un objeto. Siempre que un objeto cambia su velocidad, en términos de su magnitud o dirección, decimos que está acelerando. 

La Enciclopedia Encarta 2008 explica que la aceleración, se conoce también como aceleración lineal, y es la variación de la velocidad de un objeto por unidad de tiempo.  La velocidad se define como vector, es decir, tiene módulo (magnitud), dirección y sentido. De ello se deduce que un objeto se acelera si cambia su celeridad (la magnitud de la velocidad), su dirección de movimiento, o ambas cosas. Si se suelta un objeto y se deja caer libremente, resulta acelerado hacia abajo. Si se ata un objeto a una cuerda y se le hace girar en círculo por encima de la cabeza con celeridad constante, el objeto también experimenta una aceleración uniforme; en este caso, la aceleración tiene la misma dirección que la cuerda y está dirigida hacia la mano de la persona.

La aceleración es la razón de cambio en la velocidad respecto al tiempo. Es decir, la aceleración se refiere a cuan rápido un objeto en movimiento cambia su velocidad. Por ejemplo, un objeto que parte de reposo y alcanza una velocidad de 20 km/h, ha acelerado.  Sin embargo, si a un objeto le toma cuatro segundos en alcanzar la velocidad de 20 km/h, tendrá mayor aceleración que otro objeto al que le tome seis segundos en alcanzar tal velocidad.

Definimos la aceleración como el cambio en la velocidad respecto al tiempo durante el cual ocurre el cambio. El cambio en la velocidad (ΔV) es igual a la diferencia entre la velocidad final (V_f)y la velocidad inicial (V_i). Esto es: 

Por lo tanto definimos la aceleración matemáticamente como:

De la ecuación surge la posibilidad de que la aceleración sea positiva o negativa. La aceleración resulta ser positiva si el objeto aumentara su velocidad. Cuando el objeto aumenta la velocidad, entonces la velocidad final sería mayor que la inicial por lo que al restarlas para determinar la diferencia, la misma sería positiva. Por el contrario, si el objeto disminuye la velocidad, entonces la aceleración sería negativa. La velocidad final sería menor que la inicial y por tanto la diferencia entre ambas sería negativa. En ambos casos, si la velocidad aumenta o disminuye, decimos que el objeto está acelerado. Sin embargo es muy común utilizar la palabra desaceleración para referirnos a la aceleración negativa. 

El signo de la aceleración indica la dirección de la misma. Una aceleración positiva indica que la aceleración es en dirección al movimiento del objeto. La aceleración negativa indica que la misma es en dirección opuesta al movimiento del objeto. En próximas lecciones profundizaremos más en este aspecto. 

Si ocurriera que la velocidad final y la inicial son iguales, entonces la aceleración sería igual a cero. Para que la velocidad final y la inicial sean iguales, el objeto tendría que moverse con velocidad constante. Por lo tanto, los objetos que se mueven con velocidad constante tienen una aceleración igual a cero.

Ahora, imagina un auto que se mueve alrededor de una pista circular. Si el chófer mantiene el velocímetro, digamos que en 20 mph, el auto se estaría moviendo con rapidez constante; pero su velocidad no lo sería. Recuerda que aceleración se refiere a un cambio en la magnitud o en la dirección de la velocidad. Si el auto se mueve en una pista circular, la dirección de la velocidad cambia constantemente con la posición del auto en la pista. Por tal motivo, decimos que aunque la magnitud de la velocidad sea constante (la rapidez), la dirección de la velocidad no lo es. Por tanto, el auto estaría acelerando.

La unidad para medir la aceleración según el Sistema Internacional de Medidas es el metro por segundo cuadrado (m/s²). Recuerda que el cambio en la velocidad se mide en m/s y al dividir esta unidad por el tiempo en segundos resulta (m/s)/s o m/s². 

Cuando conocemos la aceleración de un objeto, y esta es uniforme, podemos determinar su velocidad al cabo de un intervalo de tiempo. Para ello, resolveremos la ecuación de la definición de aceleración para la velocidad final.

 Si

Esta ecuación puede ser escrita así también:

En la pasada lección discutimos que para un objeto que se mueve con velocidad constante (a = 0), la gráfica de posición versus tiempo resulta ser una línea recta, como lo muestra la figura de la derecha.  Observa el diagrama de puntos que aparece en la parte izquierda de la gráfica.  Se puede observar que la distancia entre ellos es muy similar.

Si por el contrario el objeto se mueve con aceleración uniforme distinta de cero, entonces la gráfica de posición versus tiempo resulta ser una parábola.Ese es el caso de la imagen de la derecha.  En esta puedes observar que la distancia entre los puntos va aumentando más cada vez y por lo que esa distancia no es uniforme.

En este caso, el objeto se aleja del origen aumentando la velocidad uniformemente. El aumento uniforme en la velocidad, hace que el objeto recorra mayor distancia por unidad de tiempo según se aleja. Por ello, la gráfica resulta ser una parabólica. Observa que el cambio en la posición al principio es pequeño y el mismo va aumentando según pasa el tiempo. 

Si determinamos la velocidad instantánea del objeto cada segundo, observaríamos un aumento proporcional en la misma. Por lo que la gráfica de velocidad versus tiempo sería una lineal con la pendiente igual a la aceleración.  Puedes repasar estos conceptos en la unidad de Análisis gráfico del movimiento.

II VELOCIDAD.

La velocidad también es un magnitud física vectorial que refleja el espacio recorrido por un cuerpo en una unidad de tiempo. El metro por segundo (m/s) es su unidad en el Sistema Internacional.

La velocidad media es el promedio de velocidad en un intervalo de tiempo. Para esto es necesario dividir el desplazamiento por el tiempo que se tardó en efectuarlo. Por ejemplo, si un coche tardó diez horas para recorrer una distancia de 500 kilómetros, su velocidad media fue 50 kilómetros por hora.

Se conoce como carrera de velocidad a la prueba de atletismo que consiste en correr lo más rápido posible una cierta distancia. La prueba de velocidad más popular son los 100 metros lisos o llanos, que tienen al jamaiquino Usain Bolt como hombre récord con un tiempo de 9,67 segundos.

Las carreras de velocidad también tienen lugar en el automovilismo (el automovilismo de velocidad) y el motociclismo (motociclismo de velocidad). Se trata de carreras deportivas en las cuales el objetivo es completar una cierta cantidad de vueltas a un circuito en el menor tiempo posible, o girar la mayor cantidad de vueltas en un determinado tiempo. La Fórmula 1 es un ejemplo de automovilismo de velocidad.

Las velocidades, por último, son las posiciones del mecanismo motriz de una caja de cambios: “Este cerro tienes que subirlo en primera velocidad ya que es muy empinado”.

III DIFERENCIA ENTRE VELOCIDAD Y ACELERACIÓN.

 La aceleración mide el cambio de velocidad en un móvil. El cambio de velocidad puede ser rápido, en este caso la aceleración será grande. Si la aceleración es pequeña significa que el cambio de velocidad también lo es, si la velocidad se mantiene sin cambios la aceleración será cero .

La aceleración es una magnitud vectorial que relaciona los cambios de velocidad con el tiempo que tardan en producirse. El móvil está acelerado mientras su velocidad cambie.

Aceleración constante: hay aceleración constante cuando un cuerpo recorre distancias directamente proporcional al cuidado del tiempo.

Aceleración media es el cálculo del cambio medio de rapidez

Gráfica posición-tiempo gráfica que resulta de un movimiento con velocidad constante

Gráfica que resulta del movimiento de un objeto con aceleración uniforme distinta de cero.

V   INTERPRETACIÓN Y REPRESENTACIÓN DE GRÁFICAS DE VELOCIDAD-TIEMPO Y ACELERACIÓN-TIEMPO.

Un modo de describir y estudiar los movimientos es mediante gráficas  que representan distancia-tiempo (distancia en función del tiempo), velocidad-tiempo (velocidad en función del tiempo)  y aceleración-tiempo (aceleración en función del tiempo).

Debemos anotar que los vocablos distancia, espacio y desplazamiento se usan como sinónimos.

Espacio (distancia o desplazamiento) en función del tiempo

El espacio (distancia o desplazamiento) recorrido en un Movimiento Uniformemente Acelerado (MUA) puede representarse en función del tiempo. La gráfica es una parábola cóncava ascendente.

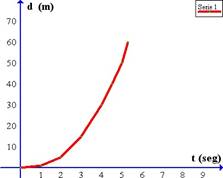
Independientemente de la forma de la parábola (cóncava o convexa en la gráfica) del movimiento los espacios que recorre el móvil son siempre positivos.

Velocidad en función del tiempo

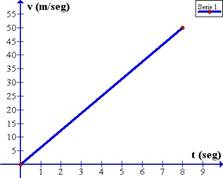
En un Movimiento Uniformemente Acelerado (MUA) la velocidad varía proporcionalmente al tiempo, por lo que la representación gráfica v-t (velocidad en función del tiempo) es una recta ascendente.

Aceleración en función del tiempo

Tal como lo dice su nombre, en el Movimiento uniformemente acelerado la aceleración es constante, por lo que la gráfica a-t (aceleración en función del tiempo) es una recta paralela al eje del tiempo, por encima de esta (la fuerza responsable de la aceleración es constante).

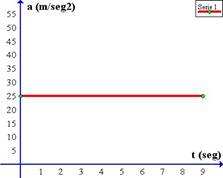
Gráfica de la aceleración en función del tiempo para un cuerpo sometido a un movimiento uniformemente acelerado.

Movimiento rectilíneo uniformemente retardado

En los movimientos uniformemente decelerados o retardados la velocidad disminuye con el tiempo de manera constante. Están, pues, dotados de una aceleración que aunque negativa es constante (la fuerza responsable de la deceleración es constante).

Por ello, todas las fórmulas cinemáticas usadas para los movimientos uniformemente acelerados sirvan para describir los movimientos uniformemente retardados, sólo que en estos casos llevan el signo negativo.

 

Espacio (distancia o desplazamiento) en función del tiempo

En los movimientos decelerados, la gráfica espacio-tiempo crece con el tiempo, pero cada vez más lentamente. La gráfica que lo representa es una parábola convexa descendente.

 

Velocidad en función del tiempo

En un movimiento uniformemente decelerado o retardado su pendiente disminuye de un modo uniforme, lo que da lugar a una gráfica velocidad-tiempo decreciente y rectilínea.

Deceleración en función del tiempo

En este tipo de movimientos la deceleración es constante, por lo que la gráfica a-t (en este caso deceleración en función del tiempo) es una recta paralela al eje del tiempo, por debajo de esta.

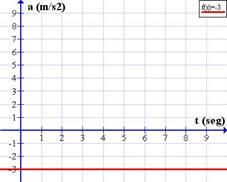
Un cuerpo que asciende

Veamos un ejemplo gráfico de un movimiento uniformemente decelerado.

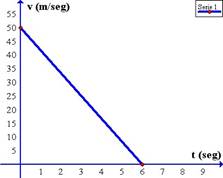
Un cuerpo lanzado verticalmente hacia arriba con velocidad inicial de 60 m/s ¿Cuál es la altura máxima que puede alcanzar?
La representación gráfica rapidez-tiempo es la siguiente:

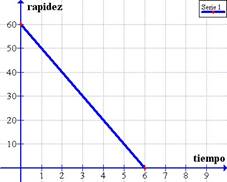
 Gráfica rapidez-tiempo para un cuerpo que asciende con una rapidez inicial de 60 m/s

¿Cómo se explica esta representación?

Veamos:

La rapidez inicial es de 60 m/s, la cual empieza a disminuir a medida que pasa el tiempo.

¿Por qué disminuye? Por influencia de la aceleración de gravedad que, redondeando, es de 10 m/s (ahora con signo negativo), entonces en cada segundo se produce una disminución de 10 m/s en la rapidez.

Aquí se puede colegir que un cuerpo que asciende con una velocidad de 60 m/s tarda exactamente 6 segundos en alcanzar la altura máxima donde se detiene por un instante antes de empezar a caer.

Al hacerlo, está partiendo de cero, y ahora su rapidez empieza a aumentar a razón de 10 m/s cada segundo, en 6 segundo alcanzará una velocidad de 60 m/s.

Esto nos demuestra que los dos movimientos son simétricos; es decir, que podemos utilizar las mismas reglas que para el caso de la caída.

http://www.youtube.com/watch?v=xQk_Dpuc0NE